You are all invited to participate in the BiCoQ seminar “The Structure and Dynamics of Massive High-z Cosmic-Web Filaments: Three Radial Zones in Filament Cross-Sections“
Speaker: Professor Nir Mandelker (The Hebrew University of Jerusalem)
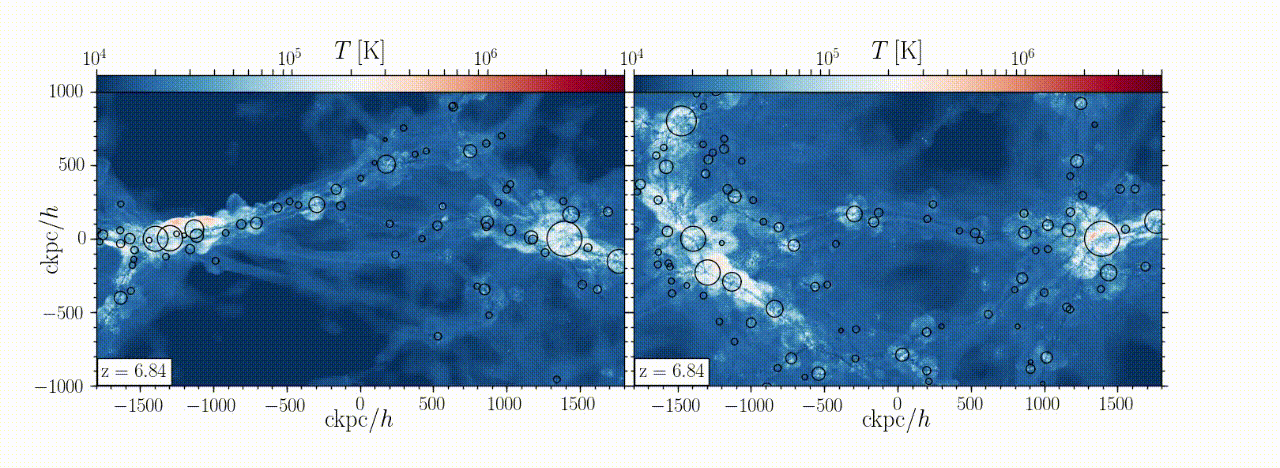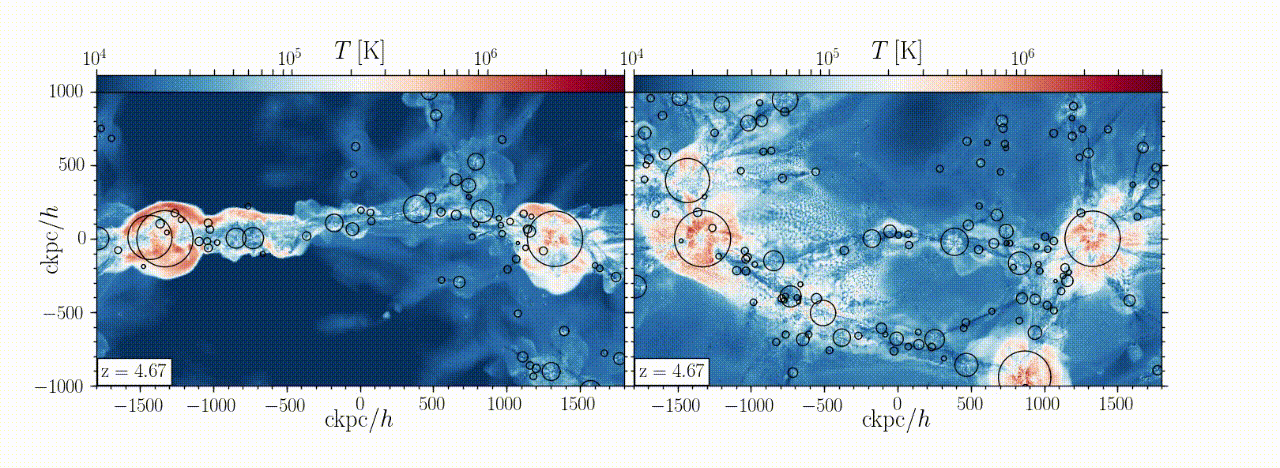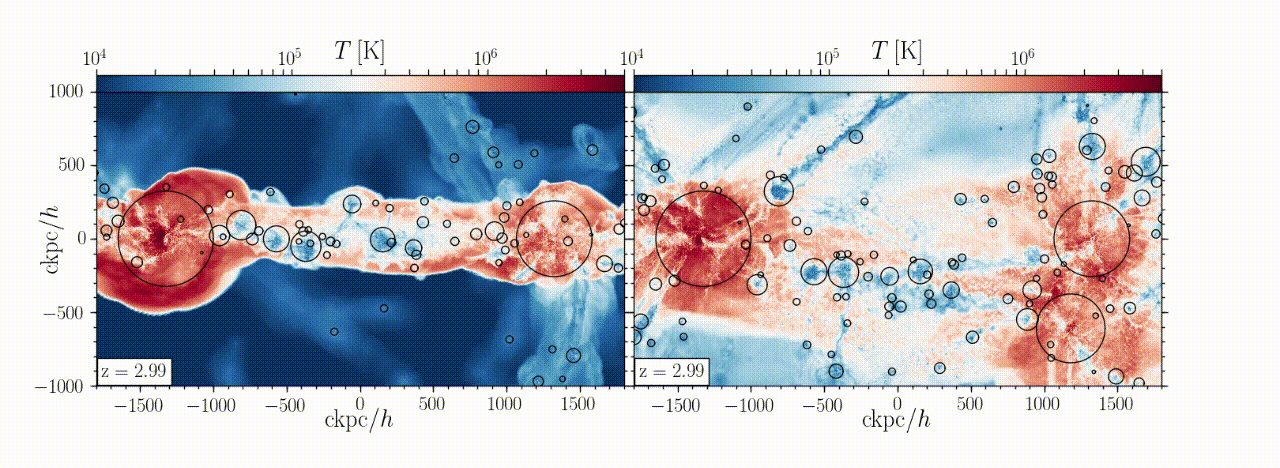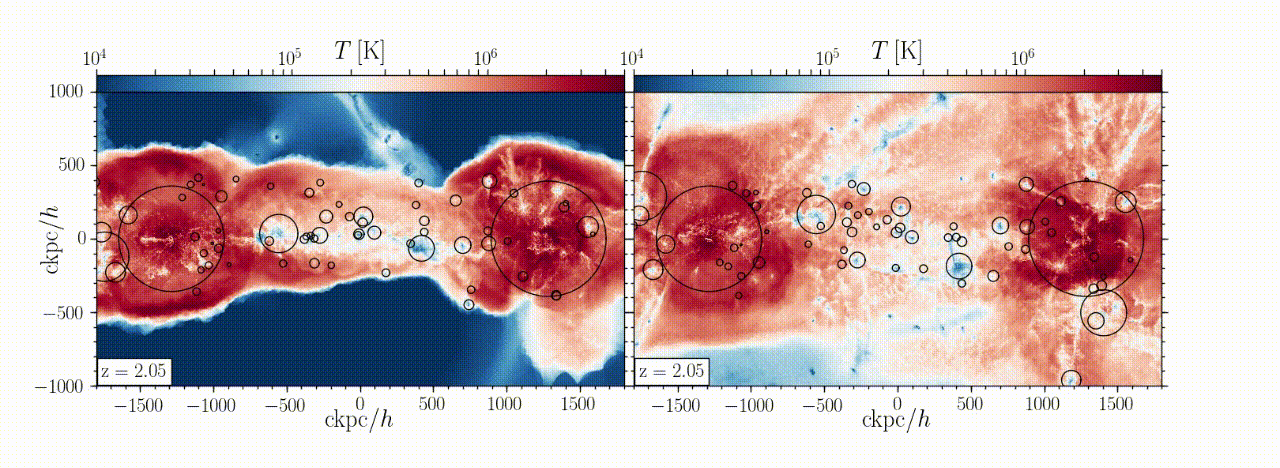
Abstract: We analyse the internal structure and dynamics of cosmic-web filaments connecting massive high-z haloes. Our analysis is based on a high-resolution AREPO cosmological simulation zooming-in on three Mpc-scale filaments feeding three massive haloes of ~10^12 Msun at z~4, embedded in a large-scale sheet. Each filament is surrounded by a cylindrical accretion shock of radius r_shock ~ 50 kpc. The post-shock gas is in virial equilibrium within the potential well set by an isothermal dark-matter filament. The filament line-mass is ~9×10^8 Msun/kpc, the gas fraction within r_shock is the universal baryon fraction, and the virial temperature is ~7×10^5 K. These all match expectations from analytical models for filament properties as a function of halo-mass and redshift. The filament cross-section has three radial zones. In the outer “thermal” (T) zone, r>~0.65 r_shock, inward gravity and ram-pressure forces are over-balanced by outward thermal pressure forces, decelerating the inflowing gas and expanding the shock outwards. In the intermediate “vortex” (V) zone, 0.25<~r/r_shock<~0.65, the velocity field is dominated by a quadrupolar vortex structure due to offset inflow along the sheet through the post-shock gas. The outward force is dominated by centrifugal forces associated with these vortices, with additional contributions from global rotation and thermal pressure. Shear and turbulent forces associated with the vortices act inwards. The inner “stream” (S) zone, r<~0.25 r_shock, is a dense isothermal core, T~3×10^4 K and nH~0.01 cm^-3, defining the cold streams that feed galaxies. The core is formed by an isobaric cooling flow and is associated with a decrease in outward forces, though exhibiting both inflows and outflows
Date/Time: Thursday, 23 May 2024, 13:30
Location: U1 – 02